An Interview On Quantum Foundations And Theoretical Physics With Tejinder Singh of TIFR

Author: Arpan Dey

Prof. Tejinder Pal Singh received a Masters in Physics from IIT Delhi in 1984 and a PhD in Physics from TIFR Mumbai in 1989. He was a post-doctoral Fellow at ICTP Trieste from 1989 to 1990. He has been a faculty member at TIFR Mumbai since 1989. He is currently a visiting professor at IUCAA.

Arpan Dey (AD): Welcome Professor Tejinder Singh of the Tata Institute of Fundamental Research (TIFR), Mumbai. So he has been doing some great work on the foundations of quantum mechanics and quantum gravity and unification. I recently listened to his talk on one of his latest works about extra time dimensions and a new theory of spacetime. So we'll be talking with him about this and a lot more, especially we'll be covering many important points in the foundations of quantum mechanics, quantum gravity and more. 

So, today we have a distinguished theoretical physicist with us, and I think this is going to be a very insightful discussion. First of all, thank you so much, sir, for your time and for agreeing to be interviewed. We're really grateful to you for your time. 

My first question to you would be what got you interested in physics? If you could go back to your childhood. Also, broadly what changes have you seen in the physics landscape from your childhood days to today? 

Tejinder Singh (TS): Thank you for having me. I can recall one or two incidents during my childhood days, which were very interesting. One was not directly related to physics or science, but a strong perception of natural beauty. My parents, me and my siblings were living in Clement Town, Dehradun, which is a very beautiful place in the lower Himalayan Hills. And that natural beauty affected me very strongly at the age of around five or six, so maybe some sense of this elegance around us in the universe was built from there. Then in 1969, I vividly remember being struck by the news that man had landed on the moon. It had a big impact on me. I knew that this was something not very usual. I was only seven years old, but it affected me in a big way.

Then the other major piece of information I can remember is when I was in grade 12. There used to be this magazine called Science Today, which no longer exists. It was an Indian science magazine. And there I understood that the stars we see in the sky are part of only our own galaxy, the Milky Way. And there are other stellar bodies, other galaxies which are outside the Milky Way. Somehow that, again, had a big impact on me that the universe is much bigger than what we see in the stars in the night sky.

And from there on, learning a little bit at the popular level that the universe began with a “big bang.” We don't know if it is true, but at least that was and still is the dominant model. And that got me interested in wanting to understand how the universe began and what was there before the beginning. And I learned in a hazy way that this has something to do with trying to find out a quantum theory of gravity. So that sort of became a motive, but it was all in the background. I mean, as my parents and my friends would suggest, I wanted to study engineering like most other people were doing at that time. So I went to engineering college and joined a five-year chemical engineering course. But after the first two years, when I was introduced to the Feynman Lectures in Physics, I realized engineering is not what I want to do. I want to do physics. Those questions came back to me. What was there before the big bang? How does one quantize gravity, whatever that meant to me at that time? So in my third year at the engineering college, I switched to physics. So nothing very profound, but just a general interest and curiosity toward understanding and solving problems of the universe. So that's that. That was 1981. So then, I did a Bachelor's and Master's in physics and so on. 

And the second part of your question, change in the landscape of physics from those days to now. So I can only comment on the part of theoretical physics, which you might call fundamental physics: foundations of quantum mechanics, the Standard Model of particle physics and our understanding of quantum gravity. So I learned all these the traditional way and did, let's say, what we can call modest mainstream research. But over the years, I have learned that in these fields, we are stuck. We have not understood or solved the foundational problems of quantum mechanics over the last one hundred years. Those problems are still with us. And I think they are very central to why we are not being able to make progress.

We have to address quantum foundations before we can make progress in quantizing gravity, before we can unify gravity with the Standard Model of particle physics, before we can understand why the Standard Model has, say, 25 or 26 dimensionless fundamental constants. I personally feel all that requires a rethink at the quantum foundational level. And that is what has guided my research. And to come back to your question, what has changed in the physics landscape? Let’s look at the mid-1970s, the Standard Model was already in place, general relativity was firmly established by then, apart from, say, the discovery of gravitational waves, which inevitably came. But after that we are stuck, the landscape is stuck. We need something radical on the theoretical side, not on the experimental side. And that's what is guiding my research along with my collaborators. 

AD: Thank you sir. In the next question, I would like to go a bit into the theory versus experiment debate. So a lot of people have this feeling that experiments have not developed to the level that we can verify the theoretical claims being made by some abstract theories like string theory. What is your view on this? Are we lacking on the theoretical or the experimental side more, and how do you think this gap between theory and experiment could be resolved?

TS: My view is that theory is way behind experiment for the following reason: experiments have already given us a lot of data, for instance, the universe appears to have one dimension of time and three dimensions of space and that their signature is opposite. This is data. You have to explain it with your theories. If we go to particle physics, we have more than 20 dimensionless fundamental constants like the low energy limit of the fine structure constant. Why is it 1/137? Then mass ratios. Why is the muon 200 times heavier than the electron? And why does the cosmological constant have the value it does? This is all data. So experimentalists have done a great job; we theorists have fallen behind. And the reason for that I believe is, again, not addressing foundational questions in physics. The quantum measurement problem, the quantum nonlocality problem, the problem of time in quantum theory. My own work suggests that when you try to start addressing these questions, you make progress toward quantum gravity and unification.

AD: There are many arbitrary parameters in the Standard Model. In one of your blogs, you talk about the strange-looking mass ratios of elementary particles. I have also read about how the mathematical structure of modular forms might naturally explain the strange features of neutrino oscillations. And there are other examples of a general mathematical structure automatically explaining a lot of things in physical theories that appear arbitrary at first glance. So do you think that in general, if we can find a general mathematical structure, then will much of this arbitrariness in physics be resolved automatically?

TS: Yeah. So again, I would come back to first addressing key questions in quantum theory. That's where we start. That guides us to what general structures we need and the central problem there, in my view, is the so-called problem of time in quantum theory. And what do I mean by that? The universe is dominated by classical macroscopic bodies like stars and galaxies. They coexist with classical spacetime. So in my picture, no classical bodies, no classical spacetime; no classical spacetime, no classical bodies. These two things go together. But we use a classical time parameter in quantum theory, which is only possible when the universe is dominated by macroscopic classical bodies. These classical objects are a limiting case of quantum theory. So it looks like quantum theory depends on its own limit. And this is true at all energy scales, including the energy scale today. Let us split apart all stars and galaxies into their fundamental constituents: electrons, quarks, neutrinos and go down to their microscopic quantum structure and imagine for a moment that the universe only consists of disjoint elementary particles and not stars and galaxies. Even in today's low energy universe, I can construct a thought experiment like that. Then it can be argued that in such a universe you will not have a classical spacetime manifold, which we can label by real number valued points. But I still need to be able to describe the dynamics of such particles. I don't have spacetime; I don't have a classical time parameter. If everything is quantum mechanical, I don't have classical spacetime even at low energies.

And this is a clue how to redo quantum theory, how to reformulate quantum theory without referring to classical time. Let us imagine that there is a way to describe the low energy universe without spacetime being labeled by real numbers. And I want to put particles in such a universe and then do quantum theory for them. Then when many of these particles get entangled in different subsets, they will form classical bodies like stars and galaxies, and then classical spacetime will emerge. The objects which are still microscopic, I can do quantum theory for them in the emergent spacetime. Spacetime emerges along with classical bodies because of the entanglement of quantum systems. The more fundamental universe must be described by a different structure of space time, which is not labeled by real numbers. So that was the guiding point. And for various reasons, we homed them in what are known as division algebras: the natural generalizations of real numbers to complex numbers, quaternions, and octonions. Real numbers, complex numbers, quaternions and octonions are the only four number systems for which division is defined, namely, if A times B is zero, then at least one of A and B must be zero. So instead of labeling space time by points, we label it by quaternions and then generalize to octonions when we want to include internal spacetime symmetries of the Standard Model of particle physics.

So each point is replaced by a quaternion, or more precisely by what is known as a split biquaternion, which takes care of chiral fermions. So in this new structure of spacetime, when you try to place particles, you cannot place fermions of arbitrary properties in a spacetime labeled by quaternions. The properties of the fermions themselves get restricted. And that is from where it seems that the apparently arbitrary dimensionless fundamental constants emerge because the structure of spacetime is now not that of real number points.

So there is a more non-trivial structure which dictates what kind of particles you can put there. Spacetime tells matter what to be. Not only does spacetime tell matter how to move, it also tells matter what to be. And it's also true that matter curves spacetime. Now the curving; it's not Riemannian geometry. It's a generalization of Riemannian geometry to non-commutative geometry. And then if you include the other forces, a further generalization to non-associative geometries; this is ongoing research. But I hope you get the picture. We seem to be making some progress toward understanding these questions. Still ongoing research, but it looks promising.

And what is very important to remember is that this has to be done at low energies also. So there are two aspects to quantum gravity. The quantum nature of the gravitational field and the non-classical nature of the spacetime manifold. Quantum gravity is not only about the gravitational field or the metric. It is also about spacetime. Other quantum forces like quantum electrodynamics or quantum chromodynamics are only about the field's quantization itself; they are not about spacetime and take spacetime as a given, fairly so. You cannot do that when you try to quantize gravity. You cannot take spacetime as a given. You have to quantize the spacetime manifold also, which means replace it by a non-real number system like quaternions.

AD: Wow! Now, I would like to talk a bit about your paper “Time-like Extra Dimensions: Quantum Nonlocality, Spin, and Tsirelson Bound”. In this paper, you suggest that there is a six-dimensional spacetime, which is actually an overlap of two four-dimensional spacetimes. One of them, I gather, is the spacetime we're familiar with, that has three space and one time dimensions. What about the other spacetime? And specifically, what is the difference between time-like and space-like dimensions in your theory?

TS: Yes. So we could start by asking why six-dimensional spacetime, where did it come from? So, in this, when we were generalizing spacetime by removing real numbers and replacing it by quaternions, we noticed one very curious thing. Fermions come with this so-called specific chirality, like there's a left-handed electron and there's a right-handed electron, and like only left-handed fermions take part in the weak interaction. So when we want to place both left-handed and right-handed fermions on this quaternionic spacetime, we realized we cannot do it with four dimensions. We have to have what are called split biquaternions, which is a doubling of quaternions in a specific way, and those are naturally associated with six-dimensional spacetimes, with three space and three time dimensions. That's how we were sort of forced to have a six-dimensional spacetime.

If you want to describe fermions and spacetime using divisional algebras, and if you want the fermions to be chiral, you are forced to have 6D spacetimes, even if you see only 4D. We know from the history of physics that what we see is not always the same as what actually is. We have to push the boundaries. So, the 6D spacetime, after the electroweak symmetry breaking in the very early universe, divides into two overlapping 4D spacetimes: the one that we are familiar with, three space and one time dimensions, and another one that we are not familiar with, which has three time and one space dimensions. One time and one space dimensions are overlapping. The other 4D spacetime has compact dimensions, much smaller than ours. They are driven by the scale of the weak force, and the spacetime curvature of the other spacetime is given by the weak force. The weak force is the left-handed analog of gravitation. Our spacetime is curved by gravity. The other spacetime is curved by the weak force, and those dimensions are very tiny. That's why we don't see those compact tiny time dimensions, which are of the order of 10^(-26) seconds. They are there, but they are too tiny, still not beyond detection.

And what is the difference between space and time dimensions? I would say only the signature. Time coordinates are like space coordinates, but they come with the opposite signature. And none of these times is the time that flows or keeps track of past, present and future. That's different, the extrinsic new time parameter coming from non-commutative geometry, which in the classical world we identify with one of these times, t1. So our 4D universe has only one of these three times. That time gets identified with the so-called time cones, the flowing time parameter. But as such, the time coordinates do not flow. They have the same status as space coordinates, and you could think of the block universe picture. If you draw a 2D spacetime diagram, x on the horizontal axis and t on the vertical, and draw a particle trajectory on this spacetime, we don't say that the particle is at x1 at time t1 and at x2 at time t2, etc. We say that the entire trajectory is given. The trajectory there pre-exists, like in the principle of least action, where you solve for the entire trajectory by extremizing the action. We are flowing through the extrinsic time parameter so as to be at (x1,t1) at an extrinsic time 𝜏1 and at (x2,t2) at an extrinsic time 𝜏2, but the entire trajectory is given, the universe is already given its history. In that picture, it is easier to understand time coordinates as being on par with the space coordinates.

AD: So this 6D spacetime is an overlap of two 4D spacetimes, and one space and one time dimensions are common to both the space time. 

TS: Yes, yes. But what we have to be careful about is what we call the spacetime metric. The spacetime metric in our 4D spacetime is very different from the spacetime metric in the other 4D spacetime. And distances and time intervals in that spacetime are much smaller than our distances and time intervals. So even in this overlapping time direction, we are setting two metrics. Our metric, according to which the universe is about 14 billion years old. The other metric in which the universe is only 10^(-26) seconds old. So even in this shared direction, the extent of time is different in the two universes. 

AD: Oh okay, that is a very crucial point. And in this theory, gravity is responsible for the curvature of our 4D spacetime, and the weak force causes the curvature of the other 4D spacetime. So how do the other two fundamental forces - electromagnetism and the strong force - fit into this picture?

TS: Strong and electromagnetic forces are the internal symmetry spaces of the other 4D spacetime, and there are correspondingly two new predicted forces, which are internal symmetry spaces of our spacetime, and that is dark electromagnetism, which is the correspondence to normal electromagnetism, and strong gravity, which is the correspondence to the strong force. So we are predicting a total of six forces, and a part of the weak force and gravity are spacetime geometries.

The other four forces are internal symmetries, and for describing them, we need octonions. For the weak force and gravity, we need only quaternions, but when we want to add internal symmetry spaces and bring in the quarks, we need the octonions. So it's very beautiful. Real numbers for the classical picture. The complex numbers are important in quantum mechanics and for the two-dimensional plane, but for our spacetime, quaternions (split biquaternions) are important in the 6D picture, and for including gauge forces, the octonions. So it's nice. Real, complex, quaternion, octonions all are getting used, and no more. It's as if the universe is built very intelligently using division algebras.

AD: It's almost as if God is a mathematician...

TS: All said and done, God, or the agency that made the universe, certainly seems to be a mathematician. The universe is one particular mathematical realization of the very vast arena of mathematics. I believe that the physical and the mathematical universe are one and the same, with the physical universe being one particular realization of mathematics. Deep down, we cannot describe physical systems without mathematics. It reduces to mathematics.

Like we say that the universe is made up of atoms of spacetime matter. The only way to define those atoms of spacetime matter is to appeal to the octonions or to appeal to matrices, which are dynamical degrees of freedom, and write an action principle for these atoms of spacetime matter. And then that is it. Rest is our language or visualization, but what carries the day is mathematics, yes.

AD: Yeah, there was a very famous paper by Eugene Wigner in which he talks about the unreasonable effectiveness of mathematics in the physical sciences. So if we think about it, many mathematical theories that were developed way back without any direct application in mind, later turned out to be the framework required to study the physical universe. I recently posted a blog on my website in which I argue that the physical universe could be a subspace of a much more general mathematical space. And it's absolutely fundamental. It's not just a language. 

So my next question. We define a quaternion as A+iB+jC+kD, where A is the real direction, and B, C, D are the imaginary directions, and the complex conjugates of i, j and k equal their negatives, and the squares of i, j and k equal -1. And for the split quaternions, it is the same but the squares of i, j and k equal +1. This ensures that the norm of such expressions resemble the spacetime signature, with opposite signs for space and time dimensions. Now, my question is, why did you consider only the imaginary parts from the quaternions to build the six-dimensional spacetime, and not the real parts?

TS: Yeah, that's a very good question. My present understanding is that the real part goes for the Higgs boson. One real part for one Higgs, the other real part for a second Higgs. So we are predicting a second Higgs in the theory, and if our theory is correct, it should be looked for and found. So that's the picture. Somehow the imaginary directions are going for making a 6D spacetime and the two real directions are going for making the Higgs. That's my picture right now.

AD: So what does the second Higgs do?

TS: Yes, yes. So, the familiar Higgs in the Standard Model gives masses to particles. The second Higgs gives electric charges to particles. Unlike in conventional theory, in our work before the electroweak symmetry breaking, we only talk of a quantity which is a combination of electric charge and mass: the product of the electric charge e and the square root of the mass m. After symmetry breaking, one Higgs assigns masses to particles, and the other Higgs assigns electric charges to particles. E√m splits into E and √m.

AD: This theory is beautiful; charge also automatically comes from the framework. And the theory has a lot of predictive power also, not just explaining the data, but also making new predictions, which I think makes it testable against existing and alternative theories. And of course it is falsifiable, which is the hallmark of a scientific theory.

TS: It is falsifiable, definitely, and our goal is that we will not put anything by hand. The fundamental action principle has three constants: Planck length, Planck time, and the reduced Planck constant ℏ, which is the quantum of action. So everything in the theory should be written in units of Planck length, Planck time and ℏ. The action should be made dimensionless by dividing by ℏ, and on the right hand side in the action principle, quantities of length dimension should be scaled by Planck length, quantities of time dimension should be scaled by Planck time. So the action itself is dimensionless, and this is it.

On a quaternionic or octonionic space (octonionic if you want to include internal symmetries), we write the so-called trace dynamics action for matrix valued degrees of freedom. From here, because of the properties of octonions and quaternions, we get six forces. Yes, and you need a gauge symmetry group also. You have to start with a presumed gauge symmetry for the overall unified action principle, and that happens to be something known as E8 X E8 for various reasons, because it gives us the world that we see. Now this E8 X E8 became very popular in the 1980s as one of the promising unified gauge groups of string theory, but then for various reasons, it became less popular. It didn't seem to work, but we have revived E8 X E8, and we have a different interpretation for how the symmetry breaking should take place. And again, quantum foundational questions are playing a very important role here. How did we end up with the quaternions and octonions? Because we wanted to remove classical spacetime from quantum theory, and octonions and E8 X E8 have a very intimate connection. So that's how we have E8 X E8 as the gauge symmetry group of the fundamental theory, and with spacetime being replaced by octonionic space. So instead of having classical particles on a real number valued spacetime and quantizing the particles, we have matrix valued degrees of freedom for particles on an octonionic space, and this is already a pre-quantum theory from which what we know should emerge, and it looks promising.

AD: Okay. I remember you mentioned trace dynamics to me when we were discussing previously as well. I don't really understand what that is. So could you briefly explain what trace dynamics is all about?

TS: It's very simple to describe. We do classical mechanics with real numbers, position and momenta, q and p, and we write an action principle using real numbers. mq̇²/2 is the kinetic energy. We can make a Lagrangian for a free particle and integrate it over time. That is your action principle. Here q is a real number. Suppose I say I want to do classical mechanics now with matrices, so q becomes a matrix, it’s no longer a real number. So I take the time derivative of the matrix q, q̇, which means differentiate all the entries in the matrix with respect to time. Then I take a square of the matrix. Because q is a matrix, q̇ is a matrix and q̇² is also a matrix. I want to make an action principle, but I want my action, as usual, to be a scalar. So I then take the trace of q̇². The trace of any (square) matrix is a scalar; trace is just the sum of the diagonal entries of the matrix. Now I integrate the trace over time; my action now is the time integral of the trace, and that's where the name “trace dynamics” comes from.

I can find the equation of motion by varying this with respect to the matrix q. You will get Newton's laws. So then one might say, what's the big deal? We are doing classical mechanics with numbers, and you're doing classical mechanics with matrices. What do you gain? Why do you do it? Interestingly, very interestingly, it turns out that for some very elegant reasons, this matrix dynamics is not classical in the sense of Newtonian mechanics and special relativity. It is, in fact, even more general than quantum theory. What's the reason for that? Suppose you have ‘q’s and ‘p’s, which are matrices. Your positions and momenta are matrices, like in quantum theory, because you raise them to operators, but you are doing classical Lagrangian dynamics. Yet my ‘q’s and ‘p’s are not commuting. Their commutator is arbitrary because dynamical variables evolve according to equations of motion. The qp commutator is not subject to a constraint here. In quantum theory, however, the qp commutator is iℏ, qp - pq = iℏ. But here the qp commutator is evolving dynamically. So under certain emergent approximations, the qp commutator becomes iℏ. Quantum theory emerges from this matrix valued Lagrangian dynamics. Let's not call it classical dynamics, because that's confusing. It's a matrix valued Lagrangian dynamics which is more general than quantum theory.

So, we do this matrix valued Lagrangian dynamics on an octonionic space. So it's very beautiful. Newtonian mechanics was real numbers on a classical spacetime, real number valued ‘q’s and ‘p’s. General relativity made spacetime curved, but kept it real number- valued, and ‘q’s and ‘p’s were still classical. Quantum theory made ‘q’s and ‘p’s into matrices or operators, but kept the spacetime fixed at real number value. 

These are two different kinds of departures from Newtonian mechanics, which are in conflict with each other. If you make ‘q’s and ‘p’s into matrices, you cannot leave your spacetime as real number valued. There's a contradiction, there's a conflict. The only way to avoid that conflict is to remove the commutative nature of spacetime and replace it by non-commuting numbers like quaternions. That's why trace dynamics on a non-commutating spacetime made up of quaternions or octonions is a natural point of departure from quantum theory. If you were to bring Einstein and Schrödinger together, let's say they had a discussion and a negotiation treaty, how should we proceed from Newton? I would say, please follow trace dynamics and quaternions. Do both together, curve space time, but in a quantum way, because you are changing degrees of freedom to matrices. The curvature produced by matrices is not Riemannian geometry of classical space. But we are still doing Newtonian mechanics in philosophy. You get what I'm saying? 

AD: Yes sir. So how do we determine the elements of these matrices for q and p? 

TS: The entries of these matrices are what are known as Grassmann numbers. Grassmann numbers are anti-commuting numbers and the square of a Grassmann number is zero, if I remember it correctly. Fermions are described by matrices made up of odd grade Grassmann numbers which don't commute with each other. Bosons are described by matrices made up of even grade Grassmann numbers which commute with each other. This is the same as in quantum field theory.  

AD: I actually came across Grasman numbers when learning Feynman’s path integrals.

TS: Yes. So trace dynamics is very close in spirit to quantum field theory. It's just that we don't impose the condition that qp - pq = iℏ. We don't impose it by hand from the start. We let it emerge when we let the underlying commutator to be arbitrary. That brings a bonus: both quantum theory as well as the measurement process (the collapse of the wave function) can be tied together unified in the trace dynamics language. So trace dynamics unifies the unitary evolution aspect and the reduction aspect of quantum theory. And trace dynamics is also the natural language once you set up your spacetime to be quaternions or octonions. They go very well with each other naturally. 

AD: Okay, sir. Now I would like to talk a bit about quantum foundations, especially the question of locality and realism. So the violation of Bell's inequality means local realism cannot be true, because that was the assumption under which Bell derived his inequality. So either locality is false or realism is false, or both are false. Of course, assuming both are false would demand a lot of radical changes. So I remember in one of your talks you illustrated how the extra time-like dimensions in your theory can actually take care of non-locality; even if two events appear non-local in our 4D spacetime, they can still be local in the 6D spacetime. Could you briefly comment on this, and also, why do you think locality should be preserved over realism?

TS: We can come to both. So let's first look at locality. What we are trying to ask is, how do correlated quantum systems manage to influence each other outside the light cone? This is confirmed experimentally by the violation of Bell's inequality. Correlated quantum systems influence each other outside the light cone. So I'm not saying anything travels at the speed or faster than the speed of light, I'm not using that language. But something happens. So I use the word “influence”. And that, to my mind, is certainly in contradiction with special relativity. It should not have happened, but it is happening. And there is something to be understood; even though there is no contradiction with experiment, there is a contradiction with special relativity. How did this happen?

So when we arrived at a 6D spacetime from our particle physics unification studies, then we realized this can address the quantum non-locality puzzle because events might be local in the 6D space time, but appear nonlocal in the 4D spacetime if we project out the other two time dimensions, which are having to do with the second spacetime. And let us now look at the second spacetime curved by the weak force. Because the metric is very small, distances in this spacetime are also very small, and it's giving a second channel between the entangled particles to communicate with each other. There is a new particle associated with the fifth force, dark electromagnetism, we talked about the dark photon. So the dark photon is transmitting the influence locally, obeying special relativity through the second 4D spacetime. And even if the particles are light years apart in our 4D spacetime, they are only about 10^(-16) centimeters apart in the other spacetime. And the dark photon travels very quickly between these particles, but we don't know that the dark photon is doing this. So it looks like a non-local influence in our spacetime. We call that the “quantum wormhole”, just to make it sound nice. There's a quantum wormhole connecting the entangled particles. Speed is not super luminal, it is the speed of light. But the distance is less. And time taken is around 10^(-26) seconds. So the influence is not instantaneous. It's just too fast, and appears instantaneous in our 4D spacetime. But it takes time. It takes 10^(-26) seconds. And if we had that kind of time-sensitive technology, we would detect that it is not instantaneous. So if we can push our technology to measure time intervals of the order of 10^(-26), we might see something interesting.

AD: That’s so interesting. I think the appeal of this theory is not only because it provides a unique explanation of non-locality, but also because it explains a lot of other things. And if we have to accept a theory, we have to accept all its predictions. So it's a very unifying framework, which explains a lot of stuff and also makes new predictions. To me, it seems the future of theoretical physics could be interesting, especially if we follow the path you described, and if we can perhaps push our experimental limits a little bit.

TS: Quite a few people are now working with octonions trying to understand their role in particle physics, in gravity and in spacetime. Lesser so trace dynamics, but I think if more attention is focused to octonions and trace dynamics, we will make progress. And that is what I call a break from standard quantum field theory, normal approaches. And you asked about the change in the physics landscape. So I feel we are in good times again. We have to look at these new kinds of theoretical ideas. And it is in this sense that theory was behind, theory was lacking in new ideas. And we have to remember that these new ideas have sprung from addressing the foundational problems of quantum theory. You address those problems, you seem to be able to help particle physics and quantum gravity, which is gratifying. It is encouraging and it gives you a framework where you can explain data. And very importantly, this is not happening at the Planck scale. So in that sense, theory is behind. I'm talking about low energy physics, fine structure constant, ratio of the muon mass to the electron mass. None of this has to do with very high energy physics or Planck scale where experiments have not been done.

AD: The next question is a very speculative question, but do you think if physics developed a bit differently, suppose let's say quantum theory came before special relativity or something like that, then would it be possible that we would have reached at a very different picture from what we have today?

TS: Yeah. Just take, for example, a situation like if Newton had discovered trace dynamics, if Newton knew about octonions, he could have done all this back then. He would predict new forces, he would come up with particle physics, he would come up with quantum theory. So we have not departed from the philosophy of Newton: deterministic evolution described by mechanics. We are still doing the same Newtonian philosophy, but with new mathematical frameworks: Riemannian geometry, non-commutative geometry, division algebras, quaternions, octonions, trace dynamics. All this has come post-Newton. Now, even at the start of the 20th century we had a good understanding of octonions and we already had trace dynamics. Trace dynamics has its beginnings actually from that time, there is some evidence already that Pascal Jordan was thinking of such things. So again, if trace dynamics had been discovered in the early 20th century, things might have been different.

But we have to remember theoretical physics is driven by experiment. Quantum mechanics as it developed was describing the experimental situation of that time and fair enough. We should not say you did not do things rightly, that's why we are stuck. No, they did beautiful things. They developed quantum field theory, they developed gauge theories, they developed the Standard Model which is consistent with all data. But what in my view got neglected is quantum foundations. What we got was the “shut up and calculate” culture and the assertion that emphasizing or exploring quantum foundations will not help particle physics and general relativity. That is where I disagree. Those problems should have been given their due regard.

There are big gaps in our understanding of quantum theory and that is what I believe have held back progress in unification and quantum gravity and that's what we are grappling with now. So if this movement happens, study quantum foundations to make progress in particle physics and quantum gravity, that movement might bring about a change in the next 10 or 20 years and I think India and young Indian students can play an important role in that.

So do not just look elsewhere. What's happening there? What is the trend? What is their philosophy? No. Think for yourself. Try to break from tradition. Work on what you think is important. So decide for yourself. Are quantum foundations important or not?

In my own research, it took me 20 years to even realize that there are these kinds of problems. That measurement problem is a problem. I appreciated these problems when I was 40 years old. Until then, it was not a problem. I was with what others used to say. “He works on quantum foundations” was a derogatory remark. To work on quantum foundations was to get oneself into trouble, from the career point of view and maybe it is still like that, but we have to fight.

I would give an example. Consider Kepler. He overturned the 2,000 years old belief that planets orbit in circles. He found from four years of research on the orbit of Mars that it is not a circle. It's an ellipse. That's a break. That takes courage. So the same way, if you think quantum foundational problems are important, you have to fight. You have to have that courage. You cannot say that “No, my career will be ruined.” Do you want to save your career or do you want to be Kepler? Kepler could have saved his career by producing a circle. But such radical breaks are what make progress. So I would like to hope that India is one such place where young minds think differently, it doesn't always have to be Europe or the United States. It can be India also, why not? We have very bright youngsters who are asking questions. I'm not saying don't go abroad, but take your thoughts and impose it on the system. This is important. That's how we are making progress, by not necessarily agreeing with the mainstream. So it's a challenge. It's a battle because there's a lot of resistance. But we must respect our own ideas.

AD: Absolutely, that’s golden advice for aspiring physicists. I firmly believe if people could think for themselves, the world would be a much better place. I think that is the most important advice that can possibly be given to a young student who wants to explore the foundations of truth. Students today are generally reluctant to fight against tradition and they always want to save their career first. But that's not how breakthroughs are made. And in a life of 70 or 80 years, what matters is we do something that is important to us, not something that is validated by society or by the system.

Now, Einstein famously remarked that God does not play dice with the universe, to which some people like Niels Bohr responded by asking Einstein to stop telling God what to do. Now, fundamentally, do you think that the universe could be deterministic? Maybe we don't know everything yet, but once we find a complete theory, then it will be deterministic. Or do you think maybe there would be some amount of randomness? Or at least some features of the universe that even a unifying theory cannot explain? For instance, in quantum mechanics there is time symmetry. The information is preserved in the time evolution of any quantum system. But at the macroscopic level, when many atoms or many particles come together to form complex systems, then we move into the domain of statistical mechanics, and there is entropy and the arrow of time. Time symmetry no longer holds and some things are more likely than others. What would be your views on this?

TS: Yeah, so let's separate this into two questions. One, is the underlying world deterministic? And secondly, why is the emergent macroscoping world having an arrow of time? Let's keep the second one aside for a moment.

So if the six-dimensional spacetime picture is correct, we can restore locality. But we still have indeterminism. So what we call it is indeterministic locality; not local realism, but local unrealism, if you want, or local indeterminism, because that is still consistent with Bell's inequality. At a deeper level, we take note that trace dynamics is a deterministic theory. It's not indeterministic. Indeterminism arises in an apparent way from coarse-graining the underlying theory, like in Brownian motion. The apparent random motion is because of the ignorance of the full microscopic picture, which is deterministic. Similarly, trace dynamics is a deterministic theory underlying the randomness aspect of quantum mechanics when we make a measurement. The latter arises because of ignorance of the underlying theory, which is trace dynamics. The emergent theory and the apparent randomness, where the underlying theory is deterministic, how that will be made consistent with Bell's inequality? I still have to understand that. But in that sense, Bell's inequality would also be emergent. So we can leave that for some other day.

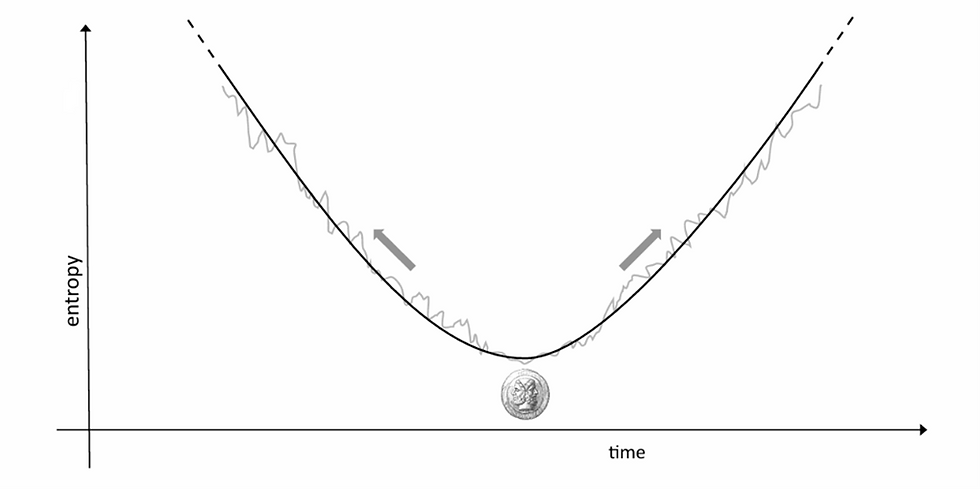
As for the arrow of time in the macroscopic world, I think it is, to my understanding, an unsolved problem. It has to do with the initial conditions at the big bang, which, as Roger Penrose emphasizes, are very special initial conditions. The Weyl curvature was zero at the big bang. The universe is homogeneous and isotropic. And Weyl curvature seems like some measure of entropy. The universe began in a low entropy state, and then the entropy increases and gives an arrow of time in the macroscopic world. But why did it begin in that special state? So that's an open question.

AD: Yes, I think it has a lot to do with the special initial conditions of the universe, like its smoothness and uniformity. Even Boltzmann, so many years back, thought about this, and probably this helped him form his past hypothesis. Although this is really an unsolved problem, because things like the Boltzmann brain are speculation, they don't have any scientific basis. But I think it has a lot to do with the initial conditions of the universe, and unfortunately we don't know anything definite about them.

So my last question to you, sir. Although you already shared some invaluable advice with us, anything else you would like to say to the present generation, the ones who want to study physics? Especially in a country like India, where physics education is still not really emphasized or encouraged as much as it should be.

TS: I would like to draw historical attention to Europe at the end of the 19th century and the beginning of the 20th century. There's this unexplained blackbody radiation spectrum, atomic spectra of atoms which are like hydrogen. These are not being explained by classical mechanics. Then the Michelson-Morley experiment. Explaining all of this required a courageous break from classical physics and tradition. That requires a great deal of courage breaking from the mainstream. Mainstream at the beginning of the 20th century was Newton. Then came Planck, Einstein, Bohr. They broke with tradition because data told them that they needed new ideas. It takes courage and vision to think differently from the rest. They were essentially loners, right? Plank, Bohr, Einstein. They were loners at the turn of the 20th century.

So I would say to young students who are interested in physics, go back and see what was happening at the beginning of the 20th century. And compare that to what's seen today. There are analogous problems. Why is the fine structure constant 1/137? Why is the muon 200 times heavier than the electron? Why are galaxy rotation curves flat? These questions don't seem to be answerable by today's “classical physics,” which is quantum mechanics and relativity. There is, again, a need to break from tradition. Be Bohr, be Einstein, be Planck. Think about what you would do to solve the most pressing problems of today. And don't go saying how to quantize gravity or how to unify the forces. Say that there is this thing that is not understood; what am I supposed to do about it to make it understood? Yeah, you see what I'm saying. I have foundational problems in quantum theory. Why does the wave function collapse? Go for these big questions. If you try to solve them, you will make progress. You'll learn good things.

AD: Absolutely, sir. So I would like to wrap up with a small comment. Today, 100 years have already passed since the birth of quantum mechanics, and yet we don't understand the foundational problems, which have been much ignored in the past. I remember reading somewhere, Daniel Greenberger made a comment that Einstein said that if quantum mechanics was correct, then the world would be crazy. Because Einstein couldn’t accept it as a complete theory and definitely it is not a complete theory in its present form, there are a lot of things we don't understand. In response Greenberger said that Einstein was right, because the world is crazy! So, if you want to make significant progress in our understanding of the universe, be crazy and don't stick to the convention. I think it was a very insightful discussion and thank you so much sir for your time.